Background

If we repeat this process for a large number of molecules we introduce a third independent process of classification or clustering. In general classification assigns a molecule to a class or set of classes on the basis of its similarity to a class prototype. The classes are independent of the set in general and a molecule may be a member of more than one class. This is the appropriate technique for diversity analysis if one is looking for "gaps", say, in one's compound collection. Clustering, on the other hand, is aimed at dividing the set up by some algorithm so that members of a cluster are more similar to each other than they are to members of other clusters. The clusters formed are set dependent. Note that the act of clustering, by its nature, forms "gaps" or "holes" in the chemical space.

If we describe our molecules by the presence or absence of features, then the binary association coefficients or similarity measures are based on the four terms a, b, c, d shown in the two way table.

Where
a is the count of bits on in object A but not in object B.
b is the count of bits on in object B but not in object A.
c is the count of the bits on in both object A and object B.
d is the count of the bits off in both object A and object B.

In addition
n = ( a + b + c + d )
A = ( a + c )
B = ( b + c )
M = ( d + c )
N = ( a + b )
U = ( a + b + c )

where
n is the total number of bits on or off in objects A or B.
A is the count of the bits on in object A.
B is the count of the bits on in object B.
M is the count of the matching bits in objects A and B.
N is the count of the non-matching bits in objects A and B.
U is the count of the bits on in objects A or B.

In the Daylight toolkit
n = dt_fp_nbits()
A = dt_fp_bitcount (fpA)
B = dt_fp_bitcount (fpB)

There are two major classes of association coefficients.

1. Those which include the double zeros i.e. d in the definitions above.
2. Those not including double zeros i.e. d in the definitions above.

Pre 4.5 releases of the Daylight software have provided an example of each of these classes.

1. The Euclidian coefficient, E is defined as the square root of the ratio
   M
   
   n
   As both M and n are functions of d, E belongs to the first class of association coefficients dependent on the double zeros.
   

2. The Tanimoto coefficient, T is defined as the ratio
   c
   
   U
   
   As U = a + b + c, T is independent of d, i.e. T belongs to the second class of association coefficients defined above.

Over the years there has been much discussion as to which type of coefficient to use. In chemistry it has generally been thought that, as most descriptor features are absent in most molecules, i.e. the bit string descriptors such as the Daylight fingerprint contains mainly zeros, coefficients such as the Tanimoto are more appropriate. However, counter arguments do exist e.g. Sokal and Sneath, in the field of numerical taxonomy, quote the following

... The absence of wings, when observed among a group of distantly related organisms ( such as a camel, a horse and a nematode), would surely be an absurd indication of affinity. Yet a postive character such as the presence of wings (or flying organs defined without qualification as to kind of wing) could mislead equally when considered, for example, for a similar heterogeneous assemblage (for example, bat, heron and dragonfly). Neither can we argue that the absence of a character may be due to a multitude of causes and that the matched absence in a pair of individuals is therefore not "true resemblance", for, after all, we know little more about the positive origins of matched positive characteristics ...

Suppose we have three objects represented by the 10 bit binary strings

          Object 1       1  0  0  0  1  1  0  0  1  0
          Object 2       0  0  0  0  1  0  0  1  1  0
          Object 3       0  0  0  0  0  0  0  1  0  0

If we were clustering this group of objects, the closest pair using Euclidian similarity would be 2 and 3; using Tanimoto, 1 and 2 are the most similar. As many hierarchical clustering algorithms start by finding the most similar pair, and in hierarchical clustering what has been put together cannot be taken apart, there is a clear need to get the appropriate measure.

These arguments also carry over to the measurement of dissimilarity. Algorithms for choosing the most diverse set, start quite frequently from the least similar pair, either measure in this case will give objects 1 and 3, but clearly that may not always be true.

This example may also be used to illustrate the associated difficulties of partition and classification. If we already had objects 1 and 3, and we wished to decide whether we associated object 2 with 1 or 3, using the Euclidian measure we would associate 2 with 3, whereas with Tanimoto we associate 2 with 1. With a large data set these problems are clearly magnified. A further example is provided by John Barnard.

Tversky similarity

... Our total database concerning a particular object is rich in content and complex in form. When faced with a comparison or identification problem we extract a limited number of relevant features on the basis of which we perform the required task ...

.......Thus the representation of of an object as a collection of features is viewed as a product of a prior process of extraction and compilation.

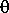S = c - a - b

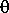
When = = 0, we are only interested that objects A and B share some features and on this measure the more features in common, the more similar the objects are. When = 1 and = 0 then we compare the features common to objects A and B with those unique to object A. The reverse is true when = 0 and = 1. When 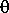= 0 and and > 0 then we are comparing the objects only on the properties they do not share, i.e. their distinguishing features. This can be regarded as a measure of distance or diversity.

The difficulty with this contrast model for the similarity measures which have developed in chemistry is that the bigger the molecule and the more unique substructures/features present the larger the similarity. A ratio model is therefore more useful and is bounded, like the Tanimoto index, between 0 and 1, irrespective of the sizes of the molecules being compared. Thus a more useful definition of the similarity S is

c

a + b + c

Note that 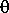becomes 1.0 in the ratio model.

There are two forms of question which we can ask,

1. Assess the degree to which object A and object B are similar to each other.
2. Assess the degree to which object B is similar to object A.

= .

In chemical terms we can now define four extreme cases

• Given a molecule A, does molecule B have any substructures in common. If = = 0, the Tversky similarity is set to 1. If there are no common substructures the index is set to zero.
  This could be useful for a potential pharmacophore filter, i.e. remove all structures that could not possibly match. The inverse list, where the index is set to zero, are compounds which are as different as possible from A which may also be useful in exploration of diversity.

• Given a molecule A, assess the degree to which molecule B is similar to it. There are two extremes:
  
  • Assess the similarity of molecule B as a superstructure of molecule A. This value is returned when = 1, = 0 and S is given by
    c
    
    a + c

    When the full set of features of A are contained in the set of features of B, a = 0 and the similarity is 1.0. This is the similarity equivalent to a superstructure match in DAYLIGHT.

  • Assess the similarity of molecule B as a substructure of molecule A. This value is returned when = 0, = 1 and S is given by
    c
    
    b + c

    When the set of features of A contain all the features of B, b = 0 and the similarity is 1.0. This is the similarity equivalent to a substructure match in DAYLIGHT.

• Given a pair of molecules A and B assess the degree to which they are similar to each other. When = = 1, the Tversky index defaults to the Tanimoto index. When = = 0.5, it returns the Dice index.

+ = 1.

c

A + B

This class of indices are linear in the shared bits c; see Z. Hubalek, Biol. Rev. (1982)57, 669-689. for a further discussion of these properties and the clustering of over 40 classification measures. Within the Daylight world, it means that indices such as the Dice coefficient are more sensitive to the shared bits than an index such as the Tanimoto, when the similarity exceeds 0.8. Note that the cosine index is also linear in c. See P. Willett et al Quant. Struct.-Act. Relat. (1995), 14(6), 501-6. for details of the use of this index.

c

sqrt(A * B)

When and/or > 1, then the distinguishing features are more important than the common ones. This could be used as a function in diversity analysis.

The question arises why do we need a sliding scale? Do intermediate values of and have any meaning other than coincidentally producing a known index such as the Dice index?

In the same way that (xv)merlin is seen as a data exploration tool, the Tversky index should be used to explore chemical similarity. If we are looking to investigate the degree to which molecule B is similar to molecule A then A is the target of the comparison, i.e. it may be regarded as the prototype. In such a task, one naturally focusses on the target of the comparison i.e. "What you know and what you know it to be about". Hence the distinctive features of the target or prototype are weighted more heavily, i.e. > and the similarity is reduced more by the distinctive features of A than of B. The degree to which this is true will vary from case to case. For example, one may wish to adjust the observed similarity of dihydroergotamine to 5-carboxamidotryptamine to reflect their similar binding at 5-hydroxytryptamine receptors. This involves decreasing the weight of the bits unique to dihydroergotamine.

5-carboxamidotryptamine

Dihydroergotamine

An example of this is provided by the work from Novartis (Euromug96).

Alternatively we may wish to cluster a set of compounds and bias the clusters so that the common features are more heavily weighted; this should drive compounds with common pharmacophores together. In this case = < 1 .

It is only by application to real cases that the true value of the Tversky index will be found. We should follow the advice of Weisberg

... I would contend that analysts frequently should not seek a single measure and will never find a perfect measure. Different measures exist because there are different concepts to measure ... It is time to stop acting embarrassed about the supposed surplus of measures and instead make fullest possible use of their diversity.

H.F. Weisberg, American Political Science Review (1974) 68, 1638-1655

Acknowledgements

and > 1

Comment from John Barnard

.....I think there is a potential confusion over the differing "sense" of Euclidean (distance) and Tanimoto (similarity), which should perhaps be clarified. Also there is the question of the need (or otherwise) to take the square root of the Euclidean Distance (as I recall, Daylight don't, in which case strictly speaking you have the Hamming Distance.

On the matter of the advantages/disadvantages of Euclidean and 1-Tanimoto (=Soergel) distances, I extend the example in the Daylight manual:
F1 and F2 each have 412 bits set, 402 of which are in common F3 and F4 each have 5 bits set, none in common. In both cases the Euclidean (Hamming) distance is 10/1024 = 0.0098 but they have widely differing Tanimoto/Soergel measures.

However (and this argues against what's in the Daylight manual) if F5 and F6 each have 412 bits set, none in common then the Tanimoto similarily for both F3/F4 and F5/F6 is 0.0 whereas their Euclidean distances are widely different, as what F3 and F4 have in common is featurelessness.