G. M. Downs and J. M. Barnard
Poster presented at Daylight EUROMUG meeting
GlaxoWellcome, Stevenage UK
1 December 1995
Barnard Chemical Information Ltd.
46 Uppergate Road
Stannington
Sheffield S6 6BX
UK.
tel. +44 114 233 3170 email: barnard@BCI1.demon.co.uk fax. +44 114 234 3415
Introduction
Since the mid-1980s, clustering of large files of chemical structures has predominantly utilised non-hierarchical methods, because these are generally faster, and require less storage space than hierarchical methods.
In particular, following extensive studies [Willett, P. Similarity and Clustering in Chemical Information Systems, Letchworth: Research Studies Press, 1987], the Jarvis-Patrick method has been widely used. An efficient implementation of the Jarvis-Patrick method is included in the Daylight Chemical Information Systems Clustering Package, and though its time complexity is O(N2) it has been used to cluster the entire SPRESI database of 2.5 million structures (which required nearly one CPU-month on a multiprocessor SGI Challenge).
The use of more efficient algorithms can reduce the complexity of some hierarchical methods from O(N3) time with O(N2) space (as required by the traditional algorithms) to O(N2) time with O(N) space; this makes such methods feasible for large databases. Clustering experiments based both on property data and on structural fingerprints suggest that hierarchical methods give much more satisfactory partitions of a large dataset.
A modification of the standard Jarvis-Patrick algorithm, which utilises variable-length nearest-neighbour lists, attempts to avoid some of the problems which are encountered with this method, such as the tendency to produce very large numbers of singletons.
Clustering methods
There are two main classes of clustering method: hierarchic methods and non-hierarchic methods. A simple classification of clustering methods is given in Figure 1.
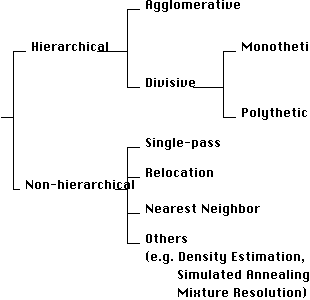
Figure 1 - A simple classification of clustering methods
Hierarchical Clustering Methods
A hierarchical clustering method produces a classification in which small clusters of very similar molecules are nested within larger clusters of less closely-related molecules.
Hierarchical agglomerative methods generate a classification in a bottom-up manner, by a series of agglomerations in which small clusters, initially containing individual molecules, are fused together to form progressively larger clusters. Hierarchical agglomerative methods are often characterised by the shape of the clusters they tend to find, as exemplified by the following range:
single-link - tends to find long, straggly, chained clusters;
Ward and group-average - tend to find globular clusters;
complete-link - tends to find extremely compact clusters.
Hierarchical divisive methods generate a classification in a top-down manner, by progressively sub-dividing the single cluster which represents an entire dataset. Monothetic (divisions based on just a single descriptor) hierarchical divisive methods are generally much faster in operation than the corresponding polythetic (divisions based on all descriptors) hierarchical divisive and hierarchical agglomerative methods, but tend to give poor results.
Hierarchical methods tend to be very demanding of computational resources,
typically
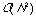to
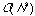for N compounds, since a complete hierarchy of partitions has to be
built-up rather than just a single partition.
One problem with these methods is how to choose which clusters or partitions to extract from the hierarchy since display of the full hierarchy is not really appropriate for datasets of more than a few hundred compounds.
Non-hierarchical Clustering Methods
A non-hierarchical method generates a classification by partitioning a dataset, giving a set of (generally) non-overlapping groups having no hierarchical relationships between them. A systematic evaluation of all possible partitions is quite infeasible, and many different heuristics have thus been described to allow the identification of good, but possibly sub-optimal, partitions.
Non-hierarchical methods are generally much less demanding of computational
resources than the hierarchic methods, typically
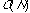to
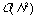for N compounds, since only a single partition of the dataset has to be
formed.
Three of the main categories of non-hierarchical method are single-pass, relocation and nearest neighbour:
single-pass methods (e.g. Leader) produce clusters that are dependent upon the order in which the compounds are processed, and so will not be considered further;
relocation methods, such as k-means, assign scompounds to a user-defined number of seed clusters and then iteratively reassign compounds to see if better clusters result. Such methods are prone to reaching local optima rather than a global optimum, and it is generally not possible to determine when or whether the global optimum solution has been reached;
nearest neighbour methods, such as the Jarvis-Patrick method, assign compounds to the same cluster as some number of their nearest neighbours. User-defined parameters determine how many nearest neighbours need to be considered, and the necessary level of similarity between nearest neighbour lists.
Other non-hierarchical methods are generally inappropriate for use on large, high-dimensional datasets such as those used in chemical applications.
Hierarchical Clustering Implementations
Two agglomerative and one divisive hierarchical clustering method have been implemented and tested. The agglomerative methods make use of Murtagh's Reciprocal Nearest Neighbour algorithm, and clustering of 150,000+ structures can be achieved in a few CPU-days on a powerful SGI Challenge. This algorithm can be applied only where the distance measure used between objects is the Euclidean Distance (Ward's method) or the Cosine Coefficient (Group-Average method).
The divisive method uses the "minimum diameter" algorithm of Guènoche et al. [J. Classification, 1991, 8, 5-30], and requires O(N2logN) time and O(N2) space; it thus remains the most computationally-intensive of the methods studied. At each step, the existing cluster with the largest diameter (maximum distance between any pair of its members) is selected for subdivision; it is divided so that the diameter of the larger of its two subclusters is a minimum. The "rate-limiting step" of the process is the sorting of a file of all N(N-1)/2 inter-object distances into decreasing order of distance, which is achieved by a highly efficient implementation of Hoare's QuickSort algorithm. In a few cases this method appears slightly superior to Ward's where the number of clusters required is small (i.e. the partition selected is near the top of the hierarchy, and relatively few subdivisions have been made).
Jarvis-Patrick Clustering
In the standard version of this method, the first processing stage identifies the K nearest neighbours of each object in the dataset. Two objects, i and j then join the same cluster if all of the following conditions are met:
* i is one of the K nearest neighbours of j;
* j is one of the K nearest neighbours of i;
* i and j have at least K
of their K nearest neighbours in common;
where K and K
are user-defined parameters. In the Daylight implementation, it is possible to
omit the first of these requirements.
Among the disadvantages of the standard method are
* "outlier" objects tend to cluster together in less densely-populated areas of space
* very small (fewer than Kmin members) isolated clusters get split up into singletons
* large compact clusters can be arbitrarily subdivided
In BCI Ltd.'s implementation, two modifications have been introduced to alleviate these problems.
* a similarity threshold restricts the nearest-neighbour lists to contain only neighbours with at least the specified similarity
* nearest-neighbour lists include all neighbours with similarity greater than the threshold, and are thus of variable length
Two objects then join the same cluster if their nearest-neighbour lists have a user-specified proportion of the entries in the shorter list in common.
Some extreme outlier objects may have empty nearest-neighbour lists and are thus excluded from the clustering process altogether, and reported separately.
Initial experiments [Brown, R. D.; Martin, Y. C. "Use of structure-activity data to compare structure-based clustering methods and descriptors for use in compound selection", submitted for publication in J. Chem. Inf. Comput. Sci., 1995] suggest that these modifications can offer some improvement on the standard method (as measured by ability to separate actives from inactives), especially for diverse datasets, but it remains inferior to hierarchical methods.
Comparisons of Clustering Methods
In 1992 Chemical Abstracts Service sponsored research work at Sheffield University, which compared the Jarvis-Patrick, Ward, Group-Average and Minimum Diameter methods.
The test dataset comprised 5982 compounds represented by 29 calculated physico-chemical properties, of which the 13 least-correlated were normalised and used as descriptors. The clustering methods were tested using a leave-one-out approach to generate predicted property values for members of each resultant cluster. i.e. each cluster (with more than two members) was used to predict the property values of its members.
Correlation of observed and predicted property values over the number of clusters produced (at different levels of the hierarchy, and different settings of the Jarvis-Patrick parameters) showed that the three hierarchical methods performed very well, in marked contrast to the Jarvis-Patrick method. An example plot is shown in Figure 2.
These results were published in 1994 [Downs, G. M.; Willett, P.; Fisanick, W.; J. Chem. Inf. Comput. Sci., 1994, 34, 1094-1102] and broadly similar results have since been obtained on different data sets using wide variety of 2-D and 3-D chemical fragment descriptors [Brown, R. D.; Martin, Y. C.; J. Chem. Inf. Comput. Sci., submitted for publication, 1995].
Figure 2 - Representative comparison of observed/predicted correlation coefficients vs. number of clusters for the four clustering methods used in the CAS property dataset study
Cluster Visualisation
The Daylight "contrib" directory contains a toolkit program written by Pam Johnson of Glaxo which allows the visualisation and selection of structures and clusters which result from Daylight's Jarvis-Patrick clustering [Chemical Design Automation News, Nov/Dec 1994].
In hierarchical clustering, it is possible to choose a partition at any level of the hierarchy, and the user is thus able to specify the number of clusters required. This may be decided a priori, or a partitioning level may be chosen as a result of examining the diversity of structures within clusters at various levels of the hierarchy.
As an aid to such choice, an adapted version of Pam Johnson's program, written by Rob Brown of Abbott Laboratories, will shortly be placed in the "contrib" directory. This allows the user to view the structures in the output from hierarchical clustering programs. The program allows the user to move up and down the hierarchy, examining the structures in a particular cluster alongside those in the cluster with which it merges at the next level up. The program can be used to choose an appropriate level at which to generate a partition.
There is substantial scope for the development of sophisticated visualisation tools for the output of hierarchical clustering programs. Such tools might involve "interactive" dendrograms in which the user would be able to click on different branches to view the compounds in the specified cluster.