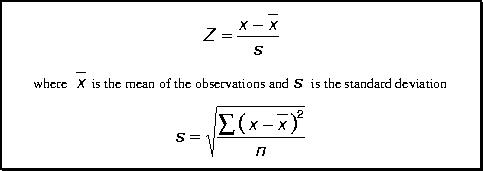
Whenever scores are expressed relative to a known mean and standard deviation they are referred to as standard scores. Z-scores are an example of standard scores as they are expressed relative to a mean of 0 and a standard deviation of 1. Another standard score is I.Q. which has a mean of 100 and a standard deviation of 15. The mathematical definition of the Z-score is

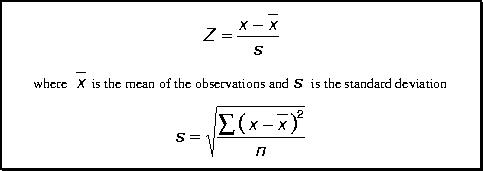
Z-scores tend to be used mainly in the context of the normal curve, and their interpretation based on the standard normal table. It would be erroneous to conclude, however, that Z-scores are limited to distributions that approximate the normal curve. Non-normal distributions can also be transformed into sets of Z-scores. In this case the standard normal table cannot be consulted, since the shape of the distribution of Z-scores is the same as that for the original non-normal distribution. For instance, if the original distribution is positively skewed the distribution of Z-scores also will be positively skewed.

Regardless of the shape of the distribution, the shift to Z-scores always produces a distribution with a mean of 0 and a standard deviation of 1.

Remember that Z-scores reflect performance relative to some group, rather than relative to an absolute standard. A meaningful interpretation of Z-score requires, therefore, that the reference group be specified.