Physiological ionization and pKa prediction

1. Abstract

2. Introduction

By varying the availability of protons, i.e. the acidity of the media, the balance of the equilibrium can be shifted. This provides a measure of the ease of proton disassociation of a site in a compound, the disassociation (or ionization) constant pKa, defined by the equation:

Alternatively, the pKa of a site can be thought of the pH at which the protonated and deprotonated fractions are equal. If the pH is higher than the pKa, the site is mostly deprotonated, and if the pH is lower than the pKa, the site is mostly protonated.

To take an example, consider the drug aspirin (acetyl salicylic acid). The structure of aspirin as given in the Merck Index, WDI or Medchem is shown on the left, CC(=O)Oc1ccccc1C(=O)O. However, the pKa of the carboxylic acid group in aspirin is 3.49, which means that under nearly all physiological conditions, this group is almost entirely deprotonated. Hence, it is the physical properties of the molecule on the right, CC(=O)Oc1ccccc1C(=O)[O-], that is of most relevant to computational chemists.

3. Ionization state vs. pKa prediction

The fact that only the physiological ionization state is required greatly simplifies and increases the applicability of pKa prediction. There is little to be gained from knowing the pKa of an ionizable group if it is significantly greater than or less than pH 7.3. Similarly, a pKa that is close to 7.3, implies that a significant fraction of the molecule may be either protonated or deprotonated, and analysis should be applied to both forms.

Consider a docking calculation of the following molecule NSC577 from NCI95. It is unlikely that there are any accurate experimental values or Hammett equations of the effects of the aromatic ring systems on the ionizable iodine, but it is clear that the site is deprotonated (by about 16 log units!).

The currently implemented algorithm to determine physiological ionization is built upon a pKa predictor. The algorithm can start from either the input or neutral form of the molecule. The method then iteratively either protonates the most basic site or deprotonates the most acidic site until there are no remaining "acid" or "base" sites for the specified pH, or until a loop is encoutered. The pKa's of all sites must be recalculated on each iteration, so that pKa reflects the ionization state of the rest of the molecule. One pleasant feature of this approach is that it can determine whether a neutral molecule is predominantly zwitterionic.

4. pKa Prediction by Atom Typing

The table below contains a number of atom types and associated values used in an atom type based predictor. The pKa is given for the both the conjugate acid and base. For convenience, the SMARTS-like constraint [!H0] is ommitted from all entries in the "Acid" column. The rows are grouped by element, and the first matching type is used. In the table below, no more than two shells of an atoms neighbour need be inspected to determine an approximate pKa.

The very generic nature of the atom types in the above table allow this approach to be applied rapidly to large datasets of diverse compounds.

5. pKa prediction by Hammett and Taft equations

This leads to the Hammett Equation for pKa:

Where Sigma is a constant assigned to a particular substituent, Rho is a constant assigned to the particular acid or base functional group and pKa⁰ is the pKa of the unsubstituted acid or base. For benzoic acids, pKa⁰ is 4.20 and Rho is defined to be 1.0.

In the original formulation, two constants need to assigned to each substituent, Sigma_meta for meta-substitutions and Sigma_para for para-substitutions. This was soon extended to aliphatic systems by Taft, by introducing Sigma_star (also written Sigma^*). Currently over 40 forms of sigma constant have been defined, but many of these corrolate extremely well with each other.

As a worked example, consider the pKa prediction of the compound shown below, 4-chloro-3,5-dimethylphenol.

The Hammett equation for phenol has pKa⁰ = 9.92 and Rho = 2.23. The Sigma_meta for -CH3 is -0.06 and the Sigma_para is 0.24. Hence the predicted value of the pKa is 9.92 - 2.23*(0.24-0.06-0.06) = 9.70. This compares extremely well with the experimental value of 9.71.

Currently, a database of over 170 Hammett/Taft equations has been encoded as SMILES/SMARTS (including chirality) from the compilation given in Perrin and Serjeant's "silver book". Similarly, a database of sigma constants for several thousand functional groups has been compiled by Corwin Hansch and Al Leo, a early TDT version of which has been placed in Daylight "contrib" by John Bradshaw.

A major benefit of Hammet/Taft equations is their ability to handle special cases.

Tetronic acids (pKa ~3.39):
The duck-billed platypus of organic chemistry?

6. Estimation of Sigma Constants

One common approach, is to extend the set of known substituents with sigma transmission equations. For example, Sigma_star of -CH2-R can be estimated as 0.41 * the Sigma_star for R. Similarly, -CH=CH- has transmission coefficient 0.51 and -C6H4- has coefficient 0.30. Similar schemes include the Exner-Fiedler method for aliphatic cycles, and the Dewar-Grisdale method for polyaromatic systems. However, this approach cannot be used when a terminal group in unparameterized.

A second approach is to use molecular orbital methods to estimate sigma values when there is no experimental data. Using the strong corrolation between sigma_meta and sigma_para and charges calculated with MOPAC's AM1 hamiltonian, Peter Ertl of Novartis has been able to calculate sigma constants for over 80,000 organic functional groups. Fortunately, as described in my MUG97 talk, "Efficient Protein and Nucleic Acid Perception", there exist efficient algorithms for pattern matching large numbers of functional groups in constant time.

7. pKa Prediction of Bound Ligands

If the neutral state of the protein is taken as the reference state, its electrostatic energy in a given ionization state is:

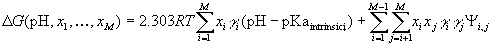
where x_i is 1 when the group i is ionized, and 0 when it is neutral; 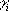is +1 for bases, and 1 for acids; pKa_intrinsic,i is the intrinsic pKa of group i; 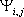is the absolute value of the interaction energy of groups i and j; M is the number of ionizable groups in the protein; R is the gas constant; and T is absolute temperature.

The intrinsic pKa of group i is given by:

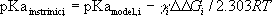
where is the difference between the free energy change of ionization for group i in the otherwise unionized protein and in a model compound of pKa_model,i. The intrinsic pKa thus represents the pKa of the group in the protein with all other titratable amino acids in the neutral state. Given values for 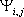and 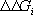for all groups, the above equation provides the basis for the computation of pH-dependent properties of protein-ligand complexes.

Traditionally, this technique has only been used for determining the protonation states of amino acid sidechains in proetins, where the values of pKa_model,i are simply looked up in a small table. However, small molecule pKa prediction methods such as those described above could easily be incorporated, not only allowing the protein the affect the ionization state of the ligand but potentially the ligand affecting the ionization state of the protein.

8. Results

SMILES	Name	Exp. pKa	Calc. pKa
	Atropine	9.90	10.3
	Chloramphenicol	11.03	15.50
	Chlorothiazide	9.50	10.10
	Chlorpromazine	9.30	10.10
	Cimetidine	6.80	5.23
	Diazepam	3.30	4.69
	Diltiazem	8.91	10.10
	Diphenhydramine	9.00	10.10
	Disopyramide	10.40	10.50
	Flufenamic Acid	3.90	4.20
	Furosemide	3.90	4.20
	Haloperidol	8.30	10.50
	Imipramine	9.50	10.10
	Lidocaine	7.94	10.50
	Phenobarbital	7.44	9.50
	Phenytoin	8.30	9.50
	Procainamide	9.40	9.25
	Propafenone	9.30	11.10
	Propranolol	9.50	11.10
	Tetracaine	8.49	10.10
	Trimethoprim	7.20	5.23
	Verapamil	9.04	10.30

The results show an impressive agreement using a very simple atom type based method. The R² value is 0.800, and a standard deviation of 0.95. Far more accurate figures on this benchmark can be achieved using Hammett & Taft equations, where ACD Labs' ACD/pKa obtains an R² value is 0.978, and a standard deviation of 0.39.

The following table shows the input and output structures of the physiological state algorithm above on the ten ligands used in Metaphorics' DockIt crunch.

PDB Code	Before	After
1HYT (-2)
1RBP (0)
1HPV (0)
1SWD (-1)
1ADD (0)
2CBR (-1)
3CLA (0)
1RDS (-1)
4HVP (+2)
1ELA (+1)

9. Bibliography

1. Jan Antosiewicz, James M. Briggs, Adrian H. Elcock, Michael K. Gilson and J. Andrew McCammon, "Computing Ionization States of Proteins with a Detailed Charge Model", Journal of Computational Chemistry, Vol. 17, No. 14, pp. 1633-1644, 1996.
2. Peter Ertl, "Simple Quantum Chemical Parameters as an Alternative to the Hammett Sigma Constants in QSAR Studies", Quantitative Structure-Activity Relationships, Vol. 16, pp. 377-382, 1997.
3. Michael K. Gilson, "Multiple-Site Titration and Molecular Modelling: Two Rapid Methods for Computing Energies and Forces for Ionizable Groups in Proteins", Proteins: Structure, Function and Genetics, Vol. 15, pp. 266-282, 1993.
4. Corwin Hansch and Albert Leo, "Exploring QSAR Vol. 1: Fundamentals and Applications in Chemistry and Biology" and "Exploring QSAR Vol. 2: Hydrophobic, Electronic and Steric Constants", ACS Professional Reference Book, American Chemical Society Publishers, 1995.
5. Bertram G. Katzung, "Basic and Clinical Pharmacology", Chapter 1, 7th Edition, Appleton and Lange Publishers, 1998.
6. D.D. Perrin, Boyd Dempsey and E.P. Serjeant, "pKa Prediction for Organic Acids and Bases", Chapman and Hall Publishers, 1981.