Daylight Clustering Manual

Copyright Notice

This document and the programs described herein are Copyright © 1992-2011, Daylight Chemical Information Systems, Inc. of Laguna Niguel, CA . Daylight explicitly grants permission to reproduce this document under the condition that it is reproduced in its entirety, including this notice. All other rights are reserved.

Table of Contents

2.1 Clustering Package Contents
2.2 Applicability
2.3 Uses of Structural Clustering

3.1 Structural Characterization
3.2 Structural Similarity
3.3 Clustering

3.3.1 Jarvis-Patrick
3.3.2 Singletons in Jarvis-Patrick
3.3.3 K-Modes
3.3.4 Sphere Exclusion
3.3.5 Scaffold-Directed

3.4 Cluster Statistics

4.1 Relationships of Cluster Package Programs
4.2 Preparing Data for Clustering
4.3 Structural Characterization
4.4 Clustering

4.4.1 Jarvis-Patrick
4.4.2 K-Modes
4.4.3 Spherex
4.4.4 Scaffold-Directed

4.5 Post-processing and Analysis

1. Intended Audience

This document should be read by everyone who intends to use the Clustering Package programs. It will also be useful for people using data generated by these programs.

This Guide is intended to provide sufficient background and information about why, when, and how the programs in the Clustering Package programs are designed to be used. Background information provided here is introductory; readers are referred to the References section of this document for more comprehensive information about structural clustering. Program syntax is not described in detail here; see the program manual pages for this information.

2. Introduction to the Daylight Clustering Package

The Daylight Clustering Package is a set of programs which provide general-purpose non-parametric clustering of objects described by an appropriate string of binary values. Commonly these will be Daylight fingerprints (see the Daylight Theory Manual), however any set of binary descriptors which fulfill the requirements of Daylight fingerprints will do. A utility program, filter_fingertalk(1) is provided to convert users descriptors into a format which will be read by Daylight applications.

2.1. Clustering Package contents

The programs supplied in this Package are batch programs which run in all Daylight supported environments except Windows. All functions needed to cluster chemical structures are provided, including data preparation, clustering parameter selection, clustering, and result post-processing. The Clustering Package thus can be used independently of any other Daylight program, however for large data sets the use of a supporting database system such as thor/merlin or DayCart is recommended.

The Daylight Clustering Package consists of nine programs:

• smi2tdt -- create file of Thor datatrees from SMILES
• fingerprint -- characterize substructural content
• nearneighbors -- find nearest neighbors by comparing fingerprints
• mergeneighbors -- combine nearest neighbors lists
• jpscan -- tabulate J-P clustering results with varying parameters
• jarpat -- Jarvis-Patrick clustering
• spherex -- Sphere exclusion selection.
• kmodes -- k-modes clustering
• showclusters -- process cluster data for textual display
• listclusters -- sort and reformat clustering data for further processing
• sdcluster -- scaffold-directed clustering

2.2 Applicability

The Daylight Clustering Package provides a set of general methods for clustering small organic compounds. However, given that the aim of clustering is to group those things together which are more similar to each other, according to the descriptor(s), than to the rest of the set, it is therefore imperative that the descriptor(s) used vary appropriately.

Jarvis-Patrick and kmodes clustering are most effective on data sets containing roughly 250 to 2,500,000 objects. Alternatively, smaller data sets are be best handled with a selection method such as spherex or scaffold-directed clustering which can handle data sets in the 1000s. Please note that usage of the cluster programs on very large data sets is limited by CPU time and memory space. While the Cluster Package programs do not impose any hard limits, e.g. clustering 10,000,000 structures is possible, but would require good hardware and a considerable length of time.

2.3 Uses of Structural Clustering

The default descriptor generator provided in the Cluster Package is the fingerprint(1) program. Daylight fingerprints are structure based representing to a first approximation the substructures present in a molecule, see below.

Structural clustering is used for a wide variety of purposes, including to:

• Automatically group compounds into structurally related families. The result is a set of clusters. This is at least a partial goal of almost all structural clustering efforts.
• Determine the degree of clustering of structures in a large set for the purpose of characterizing that set of structures. The results are the clustering statistics.
• Select a limited number of compounds to represent all structural classes in the total set for purposes such as screening for bioactivity. The result will be a set of representative compounds.
• Locate unique or unusual compounds in a set. The result is a list of compounds that don't cluster.
• Provide a very fast and compact form of similarity searching (i.e. given one structure, find all members of its cluster). The results are the cluster ID's associated with each structure.
• In Data Mining and related disciplines to discover relationships between objects in a particular descriptor space.

However, users may, if they wish, generate their own binary fingerprints, or import them from another vendors software. Indeed the objects represented need not be chemicals, for instance one could describe a set of screens by the activity/inactivity of a standard set of compounds. The Cluster Package places requirements only on the format of the fingerprint, not its content or meaning.

3. Methodology

The clustering methods used in the Daylight Clustering Package perform the following (conceptual) procedures:

• Characterize objects to be clustered in Daylight fingerprint format
• Establish inter-fingerprint similarity based on shared characteristics
• Perform non-parametric clustering based on similarity
• Post-process resultant data for improved usability

Algorithms for each of these steps are available in the graph-theory and statistical literature. Unfortunately, much of the conventional methodology lends itself poorly to the problem of chemical structure clustering. Algorithms were developed or adapted from the literature for each of these steps to achieve the general structural clustering method used in the Clustering Package.

3.1 Structural Characterization

The goal of structural characterization is to represent molecular connectivity as completely and compactly as possible in a way that lends itself to an intuitive measure of similarity.

One popular method of structural characterization is to use a fixed set of structural keys such as those used in substructure search screens. This approach was rejected as a general method as being overly biased by key selection. A certain amount of bias can be tolerated when used for substructure search as long as the user is willing to tweak the keys to match the problem, but is a terrible disadvantage for exploratory applications of cluster analysis. However, should users wish, binary keys of this type can be converted to Daylight format using the filter_fingertalk(1) program.

Another approach is to use parametric measures of molecular connectivity (e.g. the chi-index or information content). Such metrics are poor candidates for cluster analysis primarily because so little information is retained. Also, parametric measures are poorly suited to the problem: comparison of chemical structures is fundamentally a non-parametric operation. Currently Daylight does not provide conversion tools for continuous data.

The default structural characterization used in the Clustering Package is based on a binary structural fingerprint, derived as follows.

• Starting with each atom, traverse all paths, branches, and ring closures up to a certain depth (typically 8). For each substructure, derive a hash-like number from unique, relatively-prime, order-dependent contributions of each atom and bond type. Critical properties of this number are that it is reproducible (each substructure produces a single number) and its value and graph are not correlated (a linear congenital generator is used to insure this).
• Map each resulting number into a large range (typically 2K-64K) to produce a redundant, large-scale, binary representation of the substructural elements. The resultant "fingerprint" contains a large amount of information at a low density.
• Iteratively "fold" the fingerprint by OR-ing the fingerprint in half until the bit-density reaches a minimum required value or until the fingerprint reaches a minimum allowable length. The resulting fingerprint now has a high information density with a minimal (and controllable) information loss.

Fingerprints thus generated approximate a complete characterization of substructural content. The quality of the approximation is determined by their information content and density which is easily controlled. Furthermore, the information content is not biased by the generation method - fingerprints work equally well on reagents, drugs, dyes, and insecticides without any "tweaking". See the Fingerprint section of the Theory Manual for further discussion.

3.2 Structural similarity

Structural similarity is the basis of the clustering used in the Cluster Package, i.e, "similar" things should cluster together. An appropriate measure of structural similarity is thus critical to this clustering method.

Most clustering methods measure parametric similarity, typically by Euclidean distance (geometric methods) or correlation (multivariate methods). Willett (1987) examined a number of similarity coefficients, finding promise in using the tanimoto coefficient to measure similarity of chemical structures.

The tanimoto coefficient, for example, is

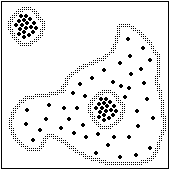
where c is the number of bits in common between fingerprint A and fingerprint B, a is the number of bits unique to A and b the number of bits unique to B. Pictorially

a = 5, b = 2, c = 19 so the tanimoto coefficient is 19/26 = 0.73. Perfect similarity would be 1.00 when a = b = 0

In recent years the Sheffield group have shown the value of other binary similarity coefficients ( see Holliday (2002) ). These are all functions of the counts a,b,c,d described below. All the usual mathematical expressions are available and described fully in expression(5)

Starting with version 4.9, the clustering package includes the ability to specify arbitrary similarity measures for the nearest neighbors list generation, spherex and kmodes clustering, and statistics computations. Similarities can be expressed in terms of bits-on-in-common c, bits-off-in-common d, and bits-on uniquely in either fingerprint a or b, being compared.

3.3 Clustering

3.3.1 Jarvis-Patrick

A very large number of clustering methods have been applied to the chemical clustering problem. The test of a clustering algorithm's effectiveness is whether it automatically classifies items of interest into groups that make sense. Although this is a subjective standard, it's clear that most of the clustering methods that have been used fail this test in the general case.

Chemical structure clustering places extremely tough demands on a clustering algorithm. For the sake of illustration, a few of these special requirements will be shown as two-dimensional parametric examples.

Many clustering algorithms are biased towards finding globular clusters. Such algorithms are not suitable for chemical clustering, where long "stringy" clusters are the rule, not the exception.

To be effective for clustering chemical structures, a clustering algorithm must be self-scaling, since it is expected to find both straggly, diverse clusters (e.g. penicillins) and tight ones (e.g. PCB's)

A chemical clustering method must be adjustable in some way that allows control of the tightness required to cluster (e.g., do the estradiols form a separate cluster within the steroid cluster or not?)

Willett published several thorough analyses and comparisons of various clustering algorithms to which the user is referred for more information (see References). One of his conclusions was that the Jarvis-Patrick method performed best, but that it was computationally prohibitive for large data sets.

The method, as published (Jarvis (1973)) works like this:

• For each item, find its J nearest neighbors. This requires order(N²) CPU time, but needs to be done only once.
• Two structures cluster together if:
  (a) They are in each other's list of J nearest neighbors, and
  (b) K of their J nearest neighbors are in common.

This method is implemented in the Clustering Package as the programs nearneighbors and jarpat. Removing clustering requirement (a) usually results in improved clustering due to a more exhaustive search but at a high cost in speed. Partially relaxing this requirement approximates the more exhaustive search and runs even faster than the published method. jarpat provides all three methods.

The Jarvis-Patrick algorithm appears to be an ideal method for clustering chemical structures:

• The same results are produced regardless of input order
• It's a non-parametric method
• Cluster resolution can be adjusted (J,K) to match a particular need
• Auto scaling is built into the method
• It will find tight clusters embedded in loose ones
• It is not biased towards globular clusters
• The clustering step is very fast
• Overhead requirements are relatively low

The main disadvantage of Jarvis-Patrick clustering is that it requires a list of near neighbors which is computationally expensive to generate, but this is effectively solved by the fast search methods provided by nearneighbors.

3.3.2 Singletons in Jarvis-Patrick

Singletons can be thought of either as structures which are not assigned to a cluster or as clusters with one member. Using reasonable rules, most sets of structures contain singletons, often 10-30% of the total. A common misconception is that singletons somehow represent a failure of the clustering process. In fact, one of the most important roles of clustering is to identify unique or unusual structures, which almost invariably appear as singletons.

For some applications, however, a large percentage of singletons is a disadvantage. For instance, consider the situation where 1,000 structures are needed to represent a database of 10,000 structures (perhaps there are resources for only 1,000 screening tests). For the purposes of this example, assume that a "natural" clustering resulted in 9,000 structures being assigned to 500 clusters leaving 1,000 singletons. Selecting 500 centroids, we now have 1,500 structures which represent the 10,000 structures in the database, which is too many. What shall we do? There are four ways of approaching this problem, roughly in decreasing order of desirability:

1. Live with the list of 1,500 produced by clustering. This sounds flippant, but is often the best solution. Attempting to force singletons into unnatural clusters will inevitably merge natural clusters which will reduce the value of cluster representatives. Consider selecting 1,000 of 1,500 based on non-structural properties, e.g. availability, price, etc.

2. Re-cluster the singletons using more lenient clustering parameters. The jarpat option -SINGLETON_FILE causes singleton structures to be written to a separate file for this purpose. Advantages of this approach are that the original "natural" clusters are unaffected, it can be pretty effective if the singleton count needs to be reduced by about half (or less), and if you later decide to do the remaining 500, you haven't messed up the sampling. Disadvantages are that singletons will be under-sampled and you will need to rerun nearneighbors on the singletons.

3. "Rescue" singletons using the jarpat option -RESCUE_SIZE <L> . Singleton rescue works as follows: clustering is done using J and K parameters as per usual; the neighbors of each singleton are then examined to see which cluster they belong to, and the singleton is added to the cluster containing the plurality of its nearest neighbors if at least L of J. Advantages of this approach are that it's fast, automatic, adjustable, it's in the spirit of the Jarvis-Patrick method, and it seems intuitively correct to many people (i.e. "rescue to nearest cluster").

4. Redo the clustering, relaxing clustering parameters such that fewer than 1,000 clusters result, including singletons. This approach does produce the best single classification of acceptable size, but be aware that many "natural" clusters will have been merged.

3.3.3 K-modes

The k-modes clustering algorithm is a variation on the commonly-used k-means non-hierarchical method suitable for non-parametric data ( Huang(1998), Chaturvedi (2001) ) The method works as follows:

• The user selects a number of clusters (K) and provides a set of K initial modals to act as starting seeds.
• An initial classification pass occurs:
  • Each item in the input dataset is assigned to the cluster such that the distance from that item to the modal for that cluster is minimized.
  • As each item is added the modal for the cluster is recomputed to include the new item.
• Zero or more relocation passes occur:
  • Each item in the input dataset is checked against the neighboring modals. If it is closer to another cluster modal, it is moved from the current cluster to the new cluster.
  • The modals for both clusters are recomputed.
• Typically relocation passes occur until no items relocate over an entire pass. When complete, each of the K clusters is output with its member items and the final modal fingerprint for that cluster.

k-modes is much less resource intensive than Jarvis-Patrick; the order of the algorithm is O(K*N), which is typically much less than the O(N^2) of Jarvis-Patrick. K-modes is a good choice for extremely large datasets and in situations where one wants to select a specific number of sample items from a dataset (K). Also, k-modes is a flexible method for simple partitioning and classification operations to select weighted subsets of a dataset rapidly. Note that, unlike Jarvis-Patrick, K-modes does depend on the input order of the dataset.

3.3.4 Sphere Exclusion

Sphere exclusion is a simple, intuitive method for compound selection ( Wooton (1975)) :

• Select one item from the dataset.
• Exclude from further consideration all items which are within a given similarity/distance threshold to the selected item.
• Repeat until all items have been selected or excluded.

Each item selected and any items excluded based on that selection are output as a cluster for further processing. The selected item is marked in the cluster.

Several variations of the method used for the item selection are available (Taylor (1995), Butina (1999)). In the classic algorithm, items are selected in the first step at random. More recently, a number of directed selections have been developed (Lee (2002)) which attempt to systematically cover the space of the dataset. The impact of the directed selection is twofold. First, the algorithm is more efficient due to locality of reference in the computation. Second, the space is more evenly covered than with the random method.

3.3.5 Scaffold-Directed Clustering

Scaffold-directed clustering is distinct from the other three clustering methods discussed above. The algorithm does not use externally supplied fingerprints but rather specifically generates a set of of fingerprints for internal use only. These fingerprints are more complex and represent longer paths by default than typical Daylight fingerprints. In addition, unlike the traditional Daylight fingerprints, they are non-hashed and easily interpreted. The agglomerative algorithm uses the internal fingerprints and a single coverage parameter to control the clustering process and thereby generate clusters which can be characterized by relatively large scaffolds shared by all members of a cluster. The final scaffolds are represented by SMARTS that may contain more than one fragment.

3.4 Cluster Statistics

Jarvis-Patrick, k-modes, and spherex clustering algorithms directly produce cluster assignments. Useful clustering statistics are number of clusters, number and percentage of structures clustered, and the frequency distribution of clusters by cluster size. Such statistics are useful for selecting clustering parameters and characterizing the set of input structures.

Since Jarvis-Patrick, k-modes, and spherex are not progressive methods, the dendogram-type of output is not relevant.

For purposes such as selecting representative structures, an intra-cluster statistic is needed to characterize the relationship of a single member to its cluster. The most frequently used statistics of this type in parametric clustering are distance from the arithmetic mean and standard error (distance/standard deviation). These statistics are not meaningful when working with non-parametric data: since it makes no sense to average bitwise data, the notion of a "mean" is meaningless. For the same reason, the variance of a cluster is not available (variance is the mean of the of squares of distances from the mean). A quantity equivalent to the variance is available in the case of k-modes where the modal acts as the "center" of the cluster.

Although we cannot determine the amount of variance unexplained by the mean for all the non-parametric methods, we can determine the amount of variance of the cluster that is unexplained by each member. This turns out to be a very useful statistic; if n is the number of members of a clusters and Cij is the similarity coefficient between members i and j, the statistic for member i is:

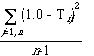
The cluster member with the lowest such statistic is the one which explains the most variance of the cluster. In geometric terms, this would be the member nearest the centroid, and should be a representative structure of the group. (This member is, perhaps loosely, called the cluster "centroid" in some of the program output.) Note that a "parent" structure is unlikelyto be a cluster centroid. Parent structures are, by definition, the least substituted structures in a group and as such are extreme members which explain very little (or none) of the within-cluster variance. This statistic is computed by the post-processing programs listclusters and showclusters.

Like the other three clustering methods, Scaffold-directed clustering directly produces cluster assignments. Useful clustering statistics that are generated include the number of clusters and number of singletons as well as the number of compounds within a cluster and the minimum scaffold coverage. In addition, the SMARTS representation of the scaffold for each cluster is provided along with the cluster members.

4. Cluster Package Usage

The following sections provide general usage instructions for programs in the Cluster Package. See the man pages for the individual programs for authoritative program syntax reference.

4.1 Relationships of Cluster Package programs

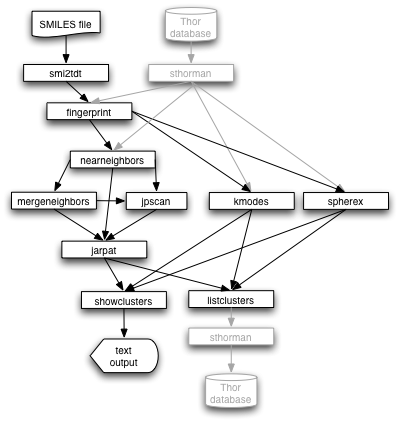
Start with either a database or with structures in SMILES. Use either sthorman or smi2tdt to generate a file of thor datatrees. The fingerprint program is used for structural characterization.

For Jarvis-Patrick clustering, the nearneighbors program is used to generate the lists of nearest neighbors for a datafile. The mergeneighbors program can be used to process and merge intermediate nearest neighbors lists. jpscan is used to determine clustering parameters, and jarpat is used to generate the cluster results.

For k-modes or Sphere Exclusion clustering, the programs kmodes and spherex, respectively, are used. Finally, the results of any of the three clustering methods are post-processed with listclusters or showclusters.

Information flow between these programs is done via Thor datatrees. This format is rigorously defined, suitable for use in many environments, allows individual programs to be used separately, and is well-suited for input to most post-processing tasks. Datatypes used include SMILES ($SMI), fingerprint (FP), near neighbors (NN), cluster (CL), and datatypes which record computed property generation ($FPG, $NNG, $CLG). Alternatively, input and output can be in SMILES format which provides a simpler format for stand-alone applications with minimal data handling needs.

4.2 Preparing Data for Clustering (smi2tdt)

The starting point for structural cluster analysis is a list of structures to be clustered. The simplest usable format that this list can take is a SMILES file, i.e. a sequential file containing one SMILES per line. Since the Clustering Package programs require Thor datatrees as input, the program smi2tdt is provided to convert SMILES format files to Thor datatree format. After clustering is completed, the program listclusters provides a means of returning the data to SMILES format if desired.

4.3 Structural Characterization (fingerprint)

The fingerprint program reads a Thor datatree containing SMILES ($SMI) rooted datatrees and adds a fingerprint (FP) dataitem to each such datatree. Fixed-size or folded fingerprints can be generated by specifying program options which include the initial size (default is 2048), the minimum size (default is 64), and minimum density (default is 0.3).

This is the same program that is used to generate fingerprints for Merlin. The default option values are set up for use in the sort of tasks that Merlin does, e.g., substructure screening and similarity searching. Fingerprints generated with the default option values contain a large amount of information at a moderate-to-high density and are suitable (if not optimal) for clustering. If available, existing fingerprints can be extracted from a database (via sthorman) rather than regenerating them with fingerprint.

Although the default fingerprints should be suitable for most databases of small organic molecules, users are encouraged to try various fingerprint parameterizations on their own data sets. Experiments indicate that the nearneighbors program works acceptably with much higher than normal fingerprint densities (e.g. generated with minimum density 0.4 or even 0.5), particularly with very large and/or highly-clustered databases. Using higher density fingerprints reduces the disk, memory, and time requirements of nearneighbors. K-modes requires the use of fixed width fingerprints in order to calculate the modal. Experiments indicate fixed width of 1024 or 2048 are fine for "drug-like" molecules. Better discrimination is found if the path length range for the fingerprint is increased to 0/8 from the default 0/7.

There is normally no need to store "specialty" fingerprints in a Thor database if they are used only to generate cluster data. Putting them in a database doesn't make them more useful for clustering and there is a potential for confusion. In any event, it is strongly recommended that a recognizable run ID be assigned to fingerprints generated with non-default parameters. For instance, using the run ID "D42" for fingerprints generated with minimum density 0.42 makes it less likely that they will be confused with standard fingerprints.

Note that all subsequent steps are performed on the fingerprints, the SMILES merely acts as a name. Users who have fingerprints generated in other ways, say a modal from a combinatorial library can take advantage of this to cluster compound libraries.

4.4 Clustering

4.4.1 Jarvis-Patrick (nearneighbors, mergeneighbors, jpscan, jarpat)

The Jarvis-Patrick clustering method is implemented in the Clustering Package as the programs nearneighbors and jarpat. The near-neighbor search is the slow step and is typically done only once. Clustering with jarpat is relatively fast but requires that appropriate clustering parameters are supplied. The program jpscan is provided to assist in selection of clustering parameters.

nearneighbors reads a Thor datatree file containing fingerprint data, copying its input to output, adding a "Nearest Neighbors" (NN) dataitem after each selected fingerprint. This program uses a bunch of computational optimizations to beat order(N²) for most chemical data sets, but it's still CPU-intensive. The optimizations work best on highly clustered data, but when running on very large data sets (e.g. 100,000+ structures), allow for the possibility of very long running time (e.g. days). It is fortunate that this step only has to be done once. Several parameters are available, the most important being the length of nearest neighbor lists to be generated (default value is 16) and the maximum list size, with ties (default value is 24). Smaller values save time and space but limit the range of clustering parameters that can be used with the results. Create lists which are as long as the largest set of neighbors to be examined, but no larger. The default value is adequate for most applications; it's rarely useful to increase it, but it can be profitably decreased when long lists aren't useful (very small data sets) or are too expensive (very large data sets).

nearneighbors can take advantage of multiple CPUs on some multiprocessing machines. This option (-NUM_PROCESSES) controls the number of child processes which get spawned on these machines. Using multiple processes decreases the overall processing time linearly with increased CPUs. mergeneighbors allows nearneighbors lists generated on the same input fingerprint files to be merged. This is extremely useful for processing of large databases. nearneighbors can be stopped and restarted at will and the intermediate lists can be easily merged.

jpscan and jarpat both perform Jarvis-Patrick clustering based on nearest neighbors (NN) data. Both programs use two Jarvis-Patrick clustering parameters: the number of neighbors to examine and the number required to be in common. jpscan repeatedly clusters data using all possible parameter combinations up to a given limit (typically set to the list length, default is 16) and outputs tables of statistics intended to help in selecting a pair of parameters appropriate to the problem at hand. jarpat requires that the parameters be specified and outputs the clustering results. It is advisable to run jpscan and examine its output before running jarpat. Both programs also allow control of the way the clustering search is done (described in section 3.3): as published (the default), an exhaustive search (only useful for very small data sets), and a faster search which approximates the exhaustive search (recommended). In addition, both programs allow the user to control how ties in similarity are handled during the clustering.

jarpat provides two (nonexclusive) methods for dealing with singletons: rescuing singletons and writing them out to a separate file. If singleton rescue is used (option -RESCUE_SIZE), rescued singletons will appear in clusters to which they are rescued. If a singleton file is generated (option -SINGLETON_FILE), it may be fed back to nearneighbors and then re-clustered.

jarpat provides an additional processing option which is not part of the original Jarvis-Patrick algorithm. This option (-NN_BEST_THRESHOLD) allows the preprocessing of the neighbors lists as follows: the best neighbor (excluding itself) for each structure is compared with the threshold value. If the best neighbor has a similarity lower than the specified threshold, then the structure is marked as a singleton and is excluded from the clustering. This is a useful way to discover very tight clusters within a dataset.

Note: nearneighbors, jpscan, and jarpat read the dataset into a fixed-size memory area (default provides room for 10,000 items) and will reallocate memory as needed to make room for more as they are read in. This memory reallocation can degrade performance on some systems. These programs provide an option to specify the number of structures to be expected - it is recommended that you use it.

4.4.2 K-modes (kmodes)

kmodes reads a Thor datatree file containing fingerprint data, and adds a cluster datatype (CL<>) with the results of the computation. In addition, it will write the modal fingerprints for each of the K clusters into the first datatree for that cluster written to output. The modal fingerprints are written with the FPM<> datatype.

Within a single run, kmodes operates on a single size of fingerprints and modals. Hence, all fingerprints and modal seeds must be of the same size on input. The program detects the size from the input dataset.

The option "-MODES <val>" controls the initial number of clusters to select (K). If during the processing a cluster falls below the value of the "-MIN_MODESIZE" option, the cluster is eliminated. Thus, the output will contain at most K clusters.

The passes are controlled with the "-MAX_PASSES" and the "-MIN_RELOC" options. The default behavior is for relocation passes to occur until no items move during a pass. This behavior can be altered by limiting the number of relocation passes with MAX_PASSES, or to stop after sufficiently small number of items relocated during a pass (expressed as a percentage of the entire dataset, using the MIN_RELOC option). If MAX_PASSES is zero, the program performs a single partitioning, writes its output, and quits.

The "-MOVE" option controls the recomputation of the modals during the initial partitioning step. The default of TRUE means that, for each item added to the cluster, the modal is recomputed. When FALSE, the modals are not recomputed as members are added to the cluster. This option only applies to the initial partitioning pass.

The initial modal seeds can be chosen from three sources. The default is to take the first K items in the dataset as the initial modals. By setting the "-RANDOM" option to TRUE, the initial modals will be selected as random members of the input dataset. Finally, the seeds can be selected from an alternate datafile with the "-SEED_FILE" option. In this case the first K fingerprints in the file will be selected as seeds.

Note: kmodes reads the dataset into a fixed-size memory area (default provides room for 10,000 items) and will reallocate memory as needed to make room for more as they are read in. This memory reallocation can degrade performance on some systems. These programs provide an option to specify the number of structures to be expected - it is recommended that you use it.

4.4.3 Sphere Exclusion (spherex)

spherex reads a Thor datatree file containing fingerprint data, and adds a cluster datatype (CL<>) with the results of the computation. It also will, for each cluster, mark the selected item (as opposed to the excluded items) with a CLT<> dataitem.

Within a single run, spherex operates on a single size of fingerprints and modals. Hence, all fingerprints and modal seeds must be of the same size on input. The program detects the size from the input dataset.

The program selects compounds from the dataset in two general modes. The default is to select compounds in order of ascending number of bits set. The second mode, controlled with the "-RANDOM" option.

For each item selected, the neighbors around it are excluded based on one of two criteria. The default criteria uses a similarity/distance threshold defined with the "-THRESHOLD", "-EXPRESSION", and "-COMPARISON" options. Please note that the "COMPARISON" option is only used in conjunction with the "EXPRESSION" option. The second exclusion criteria uses a fixed number of items based on their ranked similarity/distance, controlled with the "-SPHEREX_RANK" option.

Note: spherex reads the dataset into a fixed-size memory area (default provides room for 10,000 items) and will reallocate memory as needed to make room for more as they are read in. This memory reallocation can degrade performance on some systems. These programs provide an option to specify the number of structures to be expected - it is recommended that you use it.

4.4.4 Scaffold-Directed (sdcluster)

4.5 Post-processing and Analysis (showclusters, listclusters)

showclusters and listclusters read cluster (CL) and fingerprint (FP) dataitems in a Thor datatree (e.g. those written by jarpat). showclusters produces summaries and tables suitable for textual display or printing. listclusters reformats cluster data in a way suitable for processing by other programs. Both programs are able to sort structures by cluster and compute the intra-cluster statistics described in section 3.7.

Cluster results to be passed on to any other program should be processed by listclusters first. Aside from computing intra-cluster statistics and removing temporary data items, listclusters sorts and renumbers the clusters in a more useful, less arbitrary manner than is done by jarpat. By default, listclusters writes its output in Thor datatree format, but SMILES formatted output can be also be generated.

Although showclusters does exactly the same sorts and statistical computations as listclusters, it offers a number of summary displays and output formatting options specific to textual presentation. showclusters' output uses only printable ASCII (and newline) and is suitable for use in virtually any environment.

5. Using Clustering Data with Other Daylight Software

Thor and Merlin provide useful ways of examining cluster data. The normal procedure is to:

• Obtain your desired clustering as described above.
• Generate a Thor datatree containing SMILES ($SMI) and cluster (CL) data (via listclusters -v).
• Add the CL datatype to your datatypes database (or use one supplied with any Thor database). Be sure the POOL (_P) datafield in the datatype is set to "*;*;;*".
• Load the cluster data into a Thor database using sthorman.
• Open the database with xvmerlin. Create column(s) for cluster data and its fields as desired. All normal operations will now be available (select, sort, search, depict, save, etc.)

Merlin's function as an exploratory data analysis tool is well suited for many clustering applications. For instance, to select structures for testing, one might: create columns for "Availability", "Cost", and "Cluster ID"; remove all rows which have unacceptable "Availability", sort by "Cost"; sort by "Cluster ID" (leaves items in the same cluster sorted by cost), remove repeats in the "Cluster" column (leaving only the lowest cost, available item in each cluster), and display results.

Aside from its data analysis functions, Merlin can serve as a gateway to other programs. The "Save as text..." item in the "File" menu will write selected structures and columns to a file in tab-delimited form which is suitable for input to Daycart as well as programs such as Excel, SAS, Word, and others.

6. Maintaining Clustered Databases

The conventional method for updating nearest neighbors lists with new structures is to form a combined list, rerun nearneighbors, and re-cluster. This approach is acceptable for moderate to large databases, but it's a real limitation for very large ones.

Beginning with Release 4.34, the nearneighbors program provides the ability to update nearest neighbors lists with new structures much more quickly than starting over with all structures. To do this, use the -UPDATE_FILE (update) option to specify an file which contains previous nearneighbors output. The main advantage of this approach is speed: the full N-squared comparisons don't need to be done. Disadvantages are that you need to save the intermediate nearneighbors output (for large databases this is typically a very large file) and you must keep track of what is new since the previous run. Also understand that an "update" run uses just as much memory as a "from scratch" run and that all the nearest neighbors lists may be changed. These disadvantages do not weigh heavily when you are working with really large databases, where a full nearneighbors run might take days.

The -UPDATE_FILE option to nearneighbors subsumes the obsolete program newneighbors which was part of the original Clustering Package.

Appendix 1. Examples

Starting from a small (less than 10000 structures) .smi file containing SMILES and CAS Numbers, perform a cluster analysis and display results (Note: both old- and new-style options work):

  $ smi2tdt       -t '$CAS' smicas.smi    > smicas.tdt
  $ fingerprint    -id 7DEC smicas.tdt    > fingers.tdt
  $ nearneighbors  -FID 7DEC -NNID 7DEC fingers.tdt   > neighbors.tdt
  $ jpscan                  neighbors.tdt > /dev/printer
  $ jarpat -p 8/14 -NNID 7DEC neighbors.tdt  > clusters.tdt
  $ showclusters -h -q -v   clusters.tdt  | more
  $ showclusters -h -q -x   clusters.tdt  > /dev/printer

Repeat the above clustering, but instead of clustering with parameters 8/14, do the primary clustering with 10/16 then save, examine, and re-cluster singletons at 5/10:

  $ jarpat -NNID I -SINGLETON_FILE sin.tdt neighbors.tdt >clusters.tdt
  $ showclusters -h -q -v    clusters.tdt  > /dev/printer
  $ nearneighbors  -FID II    sin.tdt      > sing_nn.tdt
  $ jpscan                   sing_nn.tdt   > /dev/printer
  $ jarpat -JP_NEED 5 -JP_NEAR 10 -NNID II sing.nn > sing.cl
  $ showclusters -h -q -v    sing.cl   | more
  $ showclusters -h -q -x    sing.cl   > /dev/printer

Make a .smi file containing the SMILES and CAS Numbers of cluster centroids from both of the above clusterings.

  $ listclusters -d '$CAS' -s -x clusters.tdt > cents.smi
  $ listclusters -d '$CAS' -s -x sing.cl >> cents.smi
  $ cat cents.tdt > /dev/printer

Starting from .tdt file containing 80,000 SMILES with CAS Numbers perform a 6/10 cluster analysis and display cluster centroids by CAS number.

  $ fingerprint -id 4OCT smicas.tdt > fp.tdt
  $ nearneighbors -RECORD_COUNT 80000 -FID 4OCT fp.tdt > nn.tdt
  $ jarpat -JP_TYPE FAST -JP_NEED 3 -JP_NEAR 5 nn.tdt > cl.tdt
  $ showclusters -d '$CAS' -x cl.tdt | more

Prepare a .tdt file to be used to load the above results in a Thor database.

  $ listclusters -x cl.tdt > clusterdata.tdt

Appendix 2. References

D. Butina (1999) "Unsupervised Data Base Clustering Based on Daylight's Fingerprint and Tanimoto Similarity: A Fast and Automated Way To Cluster Small and Large Data Sets" Journal of Chemical Information and Computer Sciences, 39: 747-750

J. D. Carroll, A. Chaturvedi, P. E. Green (1994). "K-means, K-medians and K-modes: Special cases of partitioning multiway data." Paper presented at the Annual Meeting of the Classification Society of North America. Houston, June.

A. Chaturvedi, P. E. Green, J. D. Carroll (2001). "K-modes clustering.", Journal of Classification, 18: 35–56.

R.A. Jarvis, E.A. Patrick(1973) "Clustering Using a Similarity Measure Based on Shared Near Neighbors", IEEE Transactions on Computers, C22: 1025-1034

Z. Huang (1998) "Extensions to the k-Means Algorithm for Clustering Large Data Sets with Categorical Values", Data Mining and Knowledge Discovery 2: 283-304

J. D. Holliday, C-Y Hu, P. Willett (2002) "Grouping of coefficients for the calculation of inter-molecular similarity and dissimilarity using 2D fragment bit-strings", Combinatorial Chemistry & High Throughput Screening, 5: 155-166.

M-L. Lee (2002) "Directing Compound Selection". Retrieved March 30, 2005 from the World Wide Web: http://www.daylight.com/meetings/mug02/Lee/slides/MUG2002_DISE.html

R. Taylor (1995) "Simulation Analysis of Experimental Design Strategies for Screening Random Compounds as Potential New Drugs and Agrochemicals." Journal of Chemical Information and Computer Sciences, 35: 59-67

N. E. Shemetulskis, J. B. Dunbar, B. W. Dunbar, D. W. Moreland, C. Humblet (1995) "Enhancing the diversity of a corporate database using chemical database clustering and analysis", Journal of Computer-Aided Molecular Design 9: 407-416.

P. Willett (1987) "Similarity and Clustering in Chemical Information Systems", Letchworth, Hertfordshire, England: Research Studies Press Ltd.; 1987. 254 p. ISBN: 0-86380-050-5.

P. Willett, V. Winterman, D. Bawden (1986) "Implementation of nearest-neighbor searching in an online chemical structure search system." Journal of Chemical Information and Computer Science, 26: 109-118 .

R. Wooton, R.Cranfield, G.C. Sheppy, P.J. Goodford (1975). "Physicochemical activity relationships in practice. 2. Rational selection of benzenoid substituents" Journal of Medicinal Chemistry, 18: 607-613.

Appendix 3. Clustering Package Release Notes

All programs in the Clustering Package were revamped for Release 4.34. An additional display, "Size of largest cluster", was added to the output of jpscan. The -u (update) feature was added to program nearneighbors. Corrected a bug in programs showclusters and listclusters which resulted in incorrectly-computed "unexplained variance" statistics for some clusters based on variable-length fingerprints. Fixed bug in jpscan resulting in a floating point exception when computing average cluster size of zero (only happened with pathological distributions). Changed jarpat program so it explicitly exits with return value 0 on success so the return value can be checked in shell scripts.

Beginning with version 4.41, nearneighbors supports multiprocessing on Sun Solaris and Irix. The speed of nearneighbors has been increased by approximately 4-fold because of improvements in the fingerprint toolkit. The utility mergeneighbors has been added. jpscan now provides statistics about rescued singletons using the -RESCUE_SIZE option, and both jarpat and jpscan support the `best threshold' option. Finally, nearneighbors, mergeneighbors, jarpat, and jpscan use the new style options (e.g.. -NEIGHBORS versus -n).

In version 4.91, the kmodes and spherex methods were added.

Also in version 4.91, the options -EXPRESSION and -COMPARISON, used to define the similarity/distance measure, were added. The Jarvis-Patrick programs now generate and use variable-length nearest-neighbors lists. These lists are used to keep track of tied values in the end of a neighbors list. The option -MAX_NEIGHBORS controls the maximum size of a variable-length list, including the extra tied neighbors. The additional tied neighbors can be included or excluded from consideration during the clustering step. The option -JP_USE_ALL_TIES in jarpat and jpscan controls this.

The sdcluster program was added in version 4.93.